小孔成像

由于相机采用小孔成像的原理来采集图像，为了使图像更清晰，就采用了透镜的方式。但是因为透镜本身在成像过程中会不可避免的引入径向畸变和切向畸变（比如一条直线成像后会变成一条弧线）。为了使得现实中的图像能够真实的呈现在图片中有利于之后的机械臂的抓取，则需要对相机进行畸变校正。

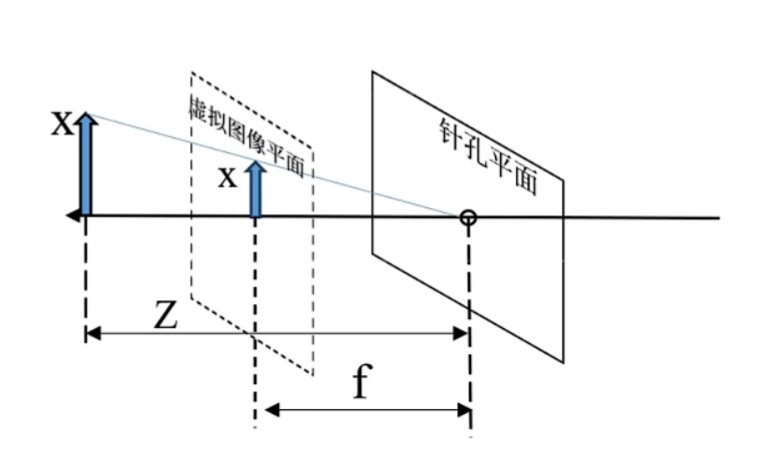
image-20250623092918445

相机的成像模型

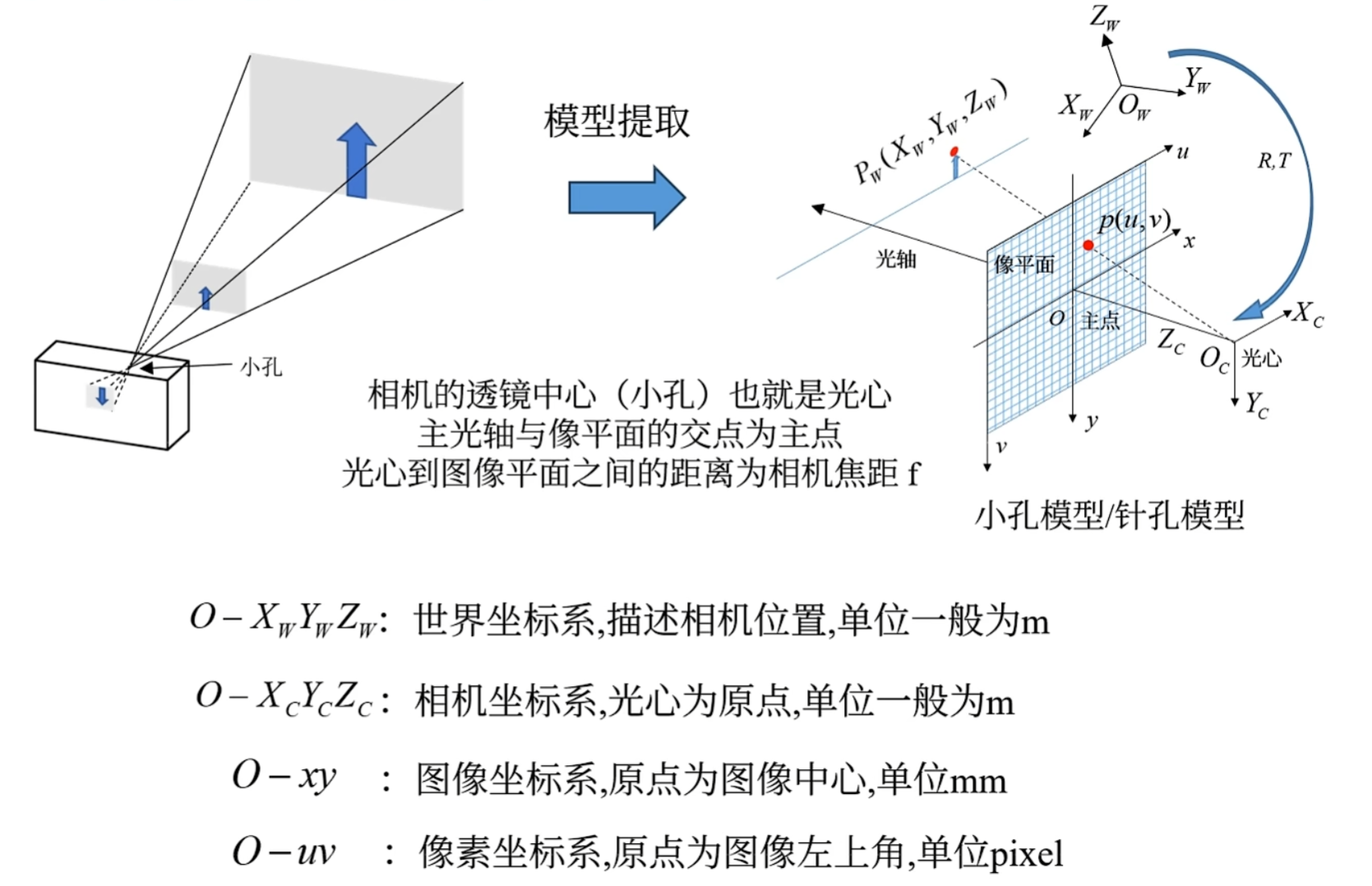
image-20250623093433508

世界坐标系是一个物体在真实三维世界下的坐标，世界坐标系的原点根据具体情况来定

相机坐标系是以相机光心为原点的三维坐标系，Zc为深度信息

图像坐标系是以图像中心为原点的二维坐标系，P点为Pw投影到像平面上的位置

像素坐标系是以图像左上角为原点的二维坐标系，好处是所有坐标都是正数

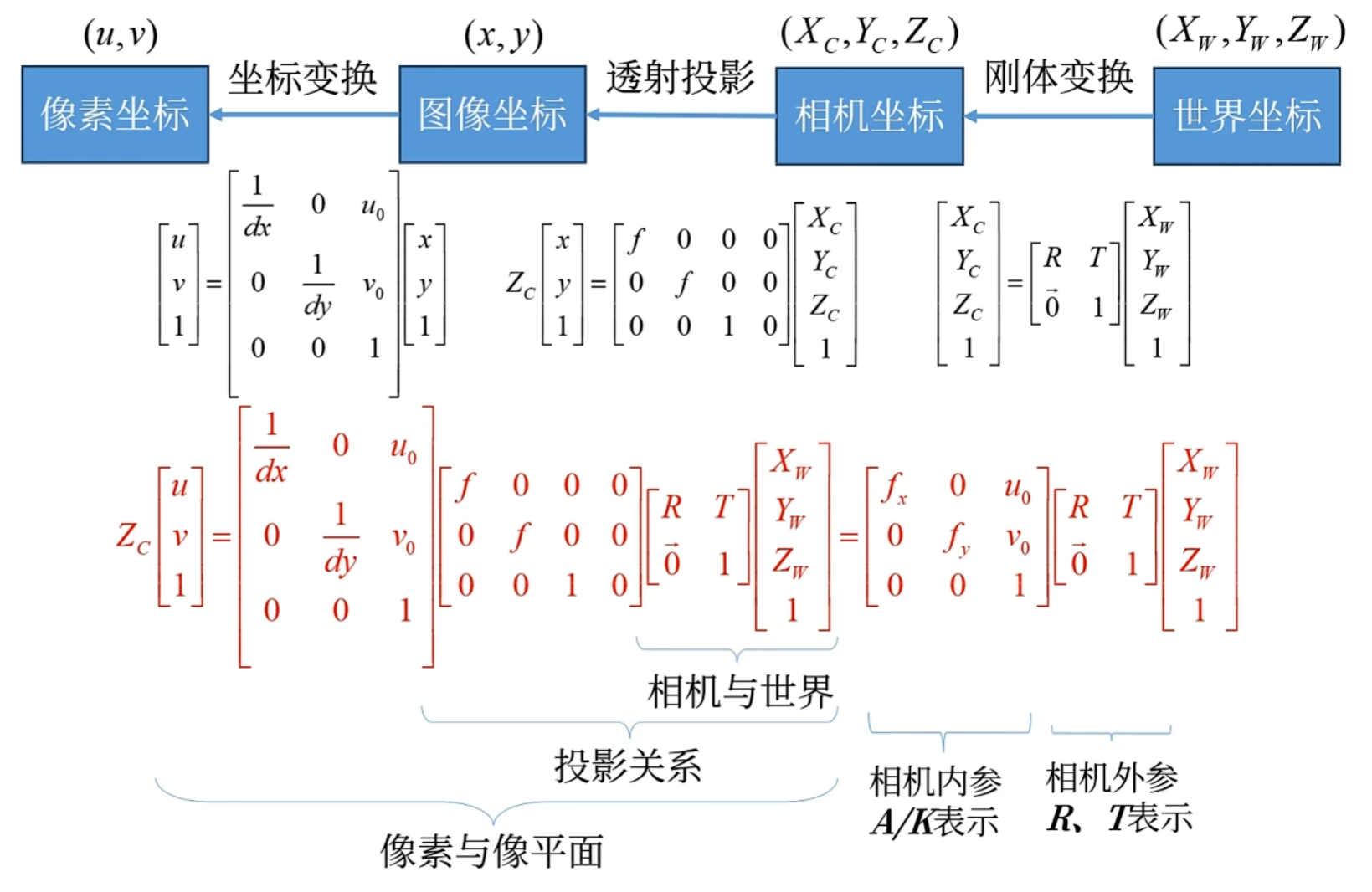
相机成像过程为，世界坐标系经过刚体变换（平移、旋转）后和相机坐标系重叠，即转换为相机坐标系。然后通过透视投影转换为图像坐标，最后经过坐标变换得出像素坐标。

世界坐标系到相机坐标系

从世界坐标系变换到相机坐标系属于刚体变换:即物体不会发生形变，只需要进行旋转和平移。思路:先进行坐标系旋转，后进行坐标系平移。

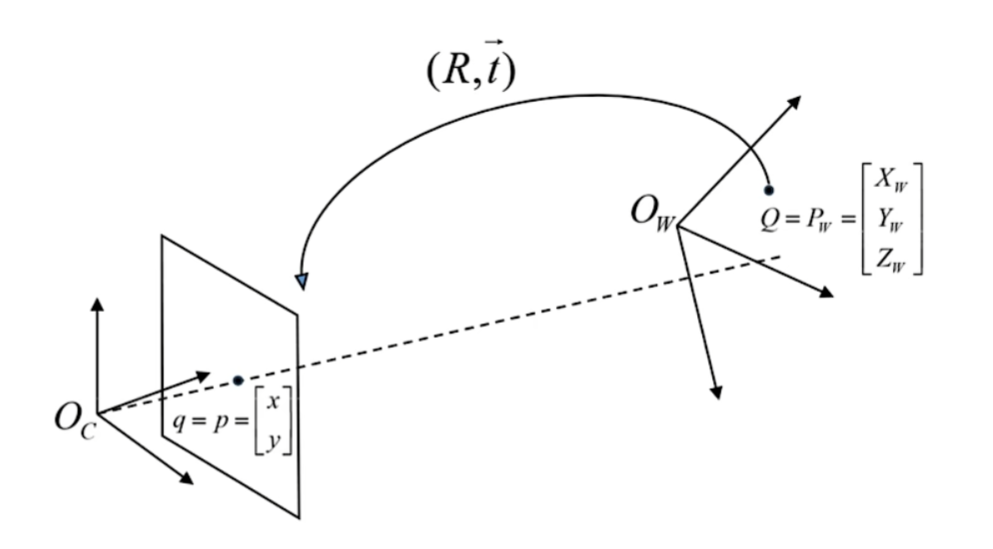
image-20250623095650474

世界坐标系通过左乘矩阵$R_z$先绕Z轴转动$\theta$角，再通过左乘矩阵$R_y$绕Y轴转动$\beta$角,最后通过左乘矩阵$R_x$绕X轴转动$\alpha$角。于是可以得到旋转矩阵$R=R_xR_yR_z$。

image-20250623100151430

经过一系列的旋转，世界坐标系和相机坐标系的朝向一致，经过平移可以让两个坐标系重合。平移向量为世界坐标系原点减去相机坐标系原点。将平移和旋转叠加起来得到下式：

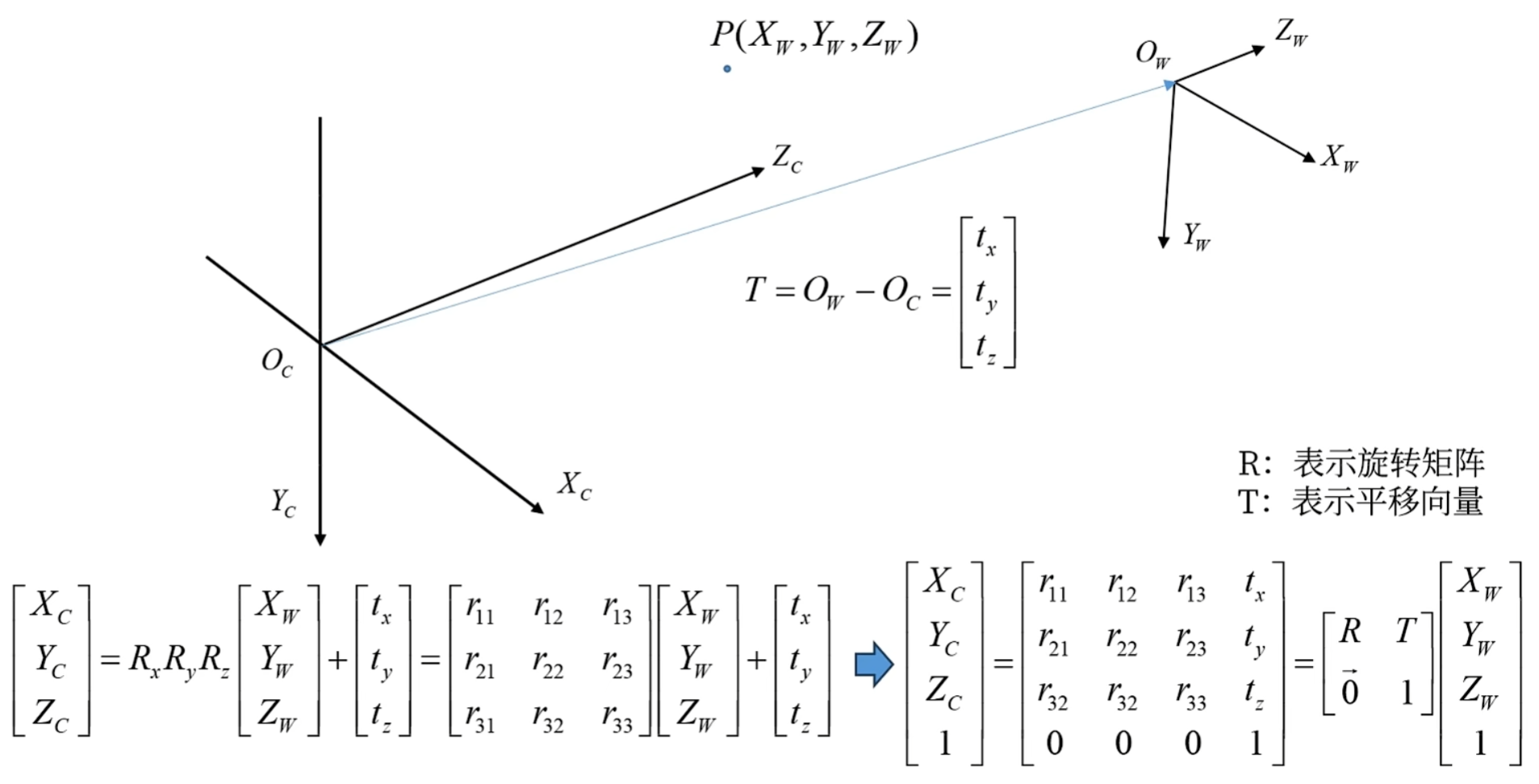
image-20250623102307173

相机坐标系到图像坐标系

透视投影(perspective projection): 用中心投影法将形体投射到投影面上，从而获得的一种较为接近视觉效果的单面投影图，有一点像皮影戏它符合人们心理习惯，即离视点近的物体大，离视点远的物体小。

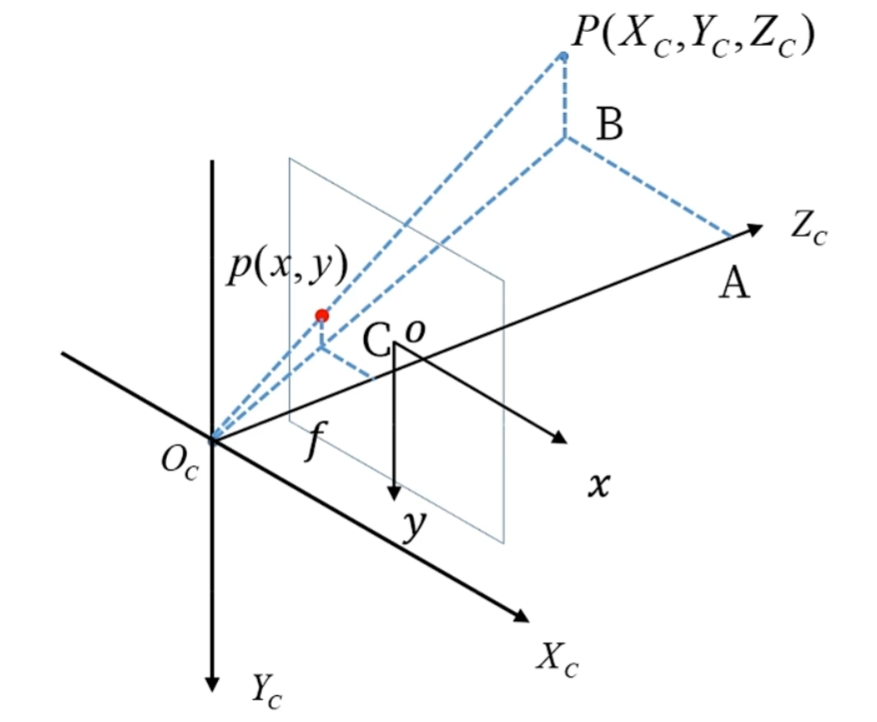
image-20250623095821120

根据相似三角形原理可得：

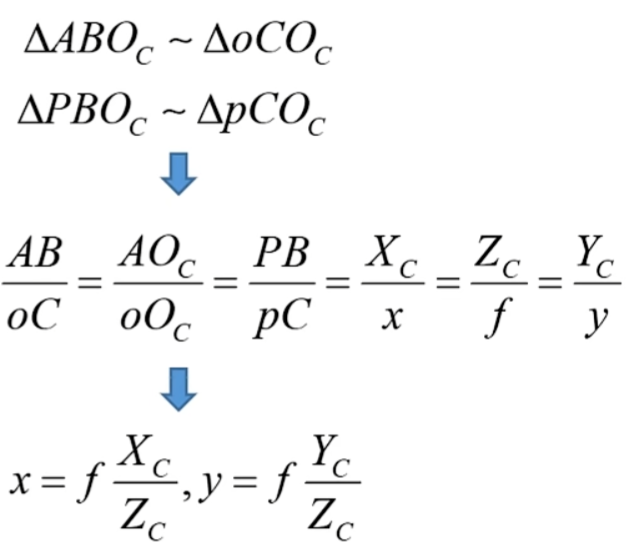
image-20250623095834551

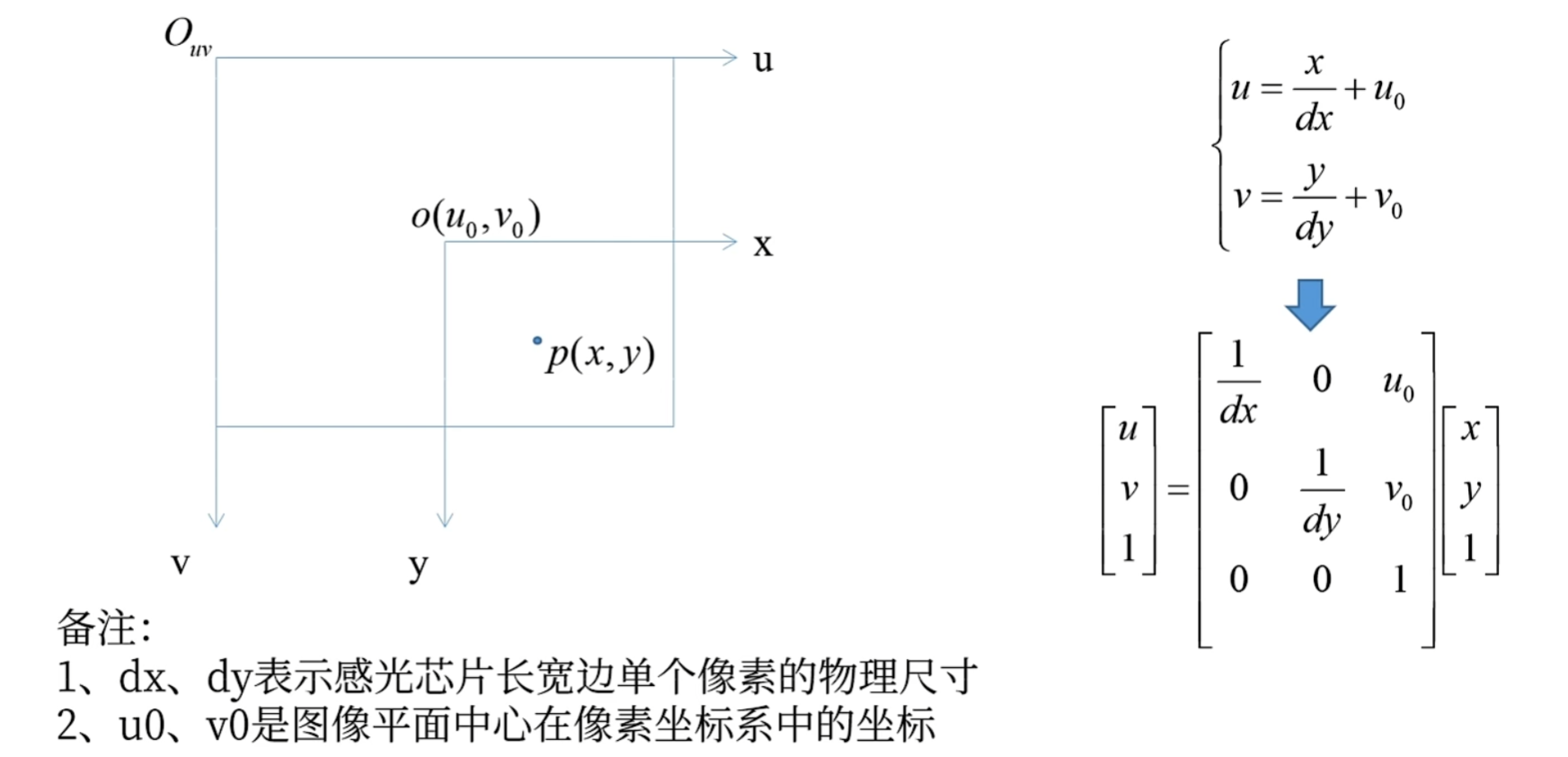
图像坐标系到像素坐标系

image-20250623110251861

理想相机数学模型

image-20250623110327011

相机畸变

畸变分为桶形畸变和枕形畸变。

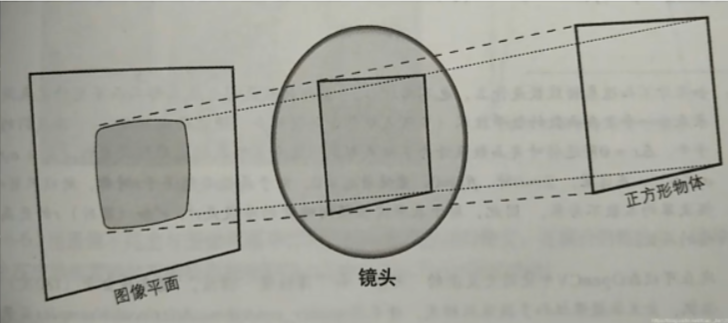
image-20250623112449899

image-20250623112254217

另外在相机装配过程中成像芯片可能和镜头不平行，最后图像可能发生倾斜畸变

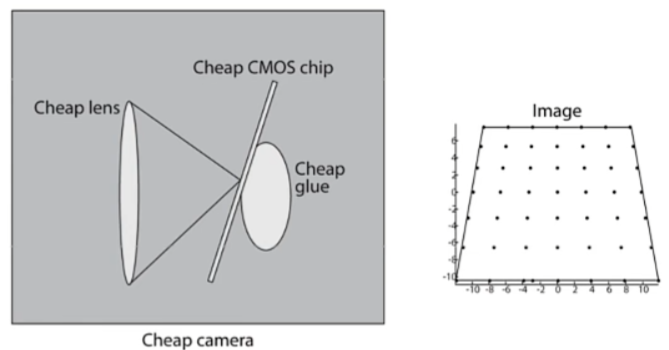
image-20250623112537402

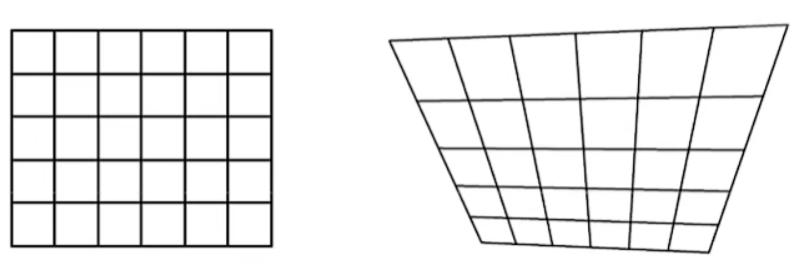
image-20250623112556946

畸变模型

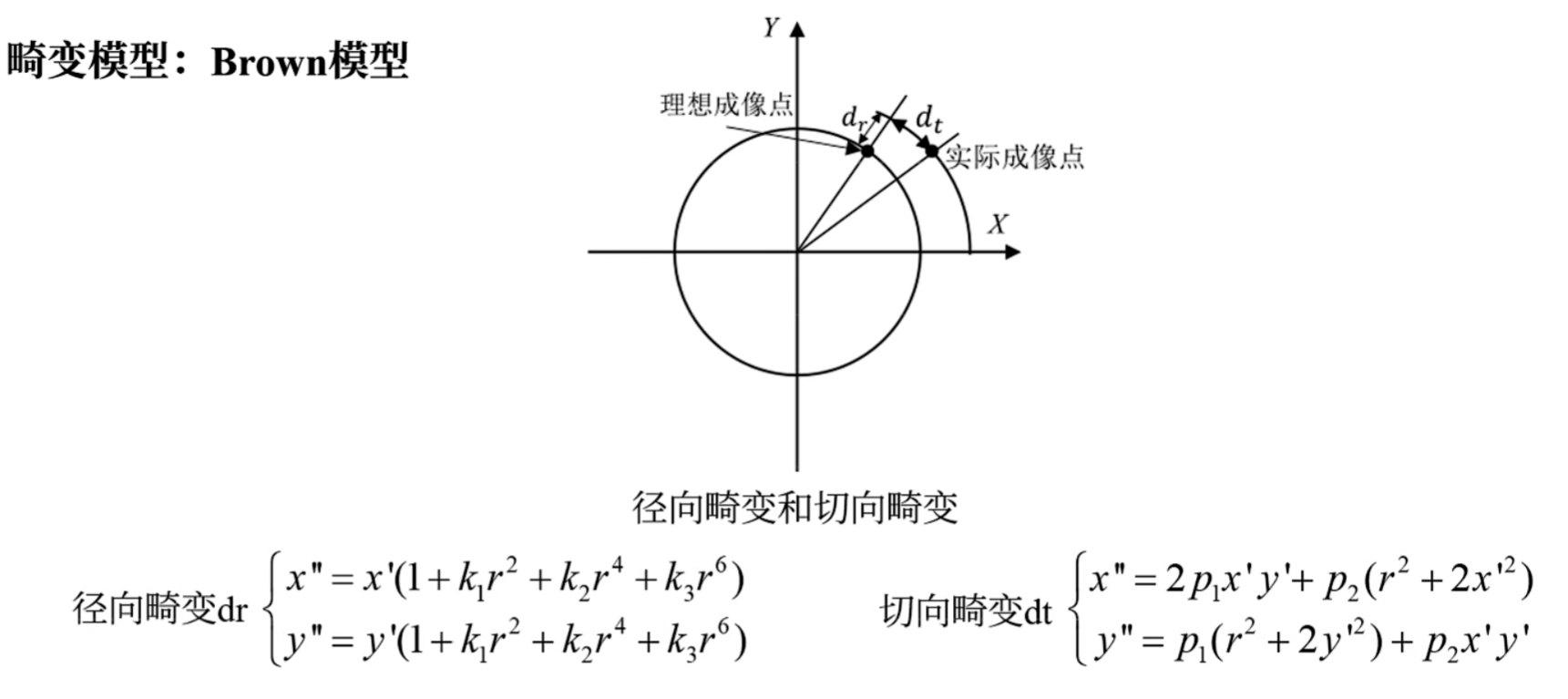
image-20250623112642409

两种畸变公式叠加起来得到最后的畸变公式

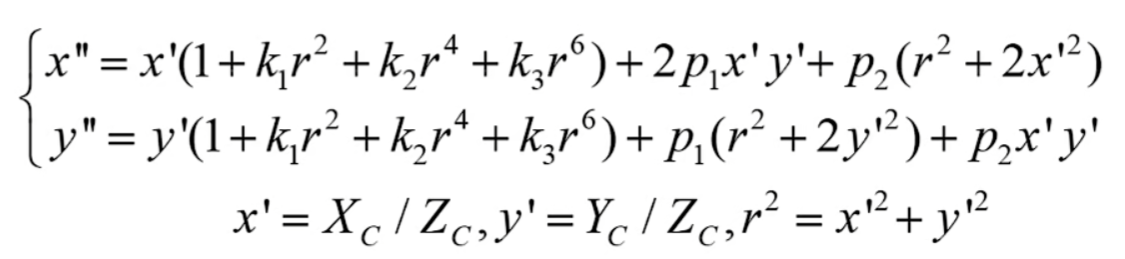
image-20250623112733653

模型总结

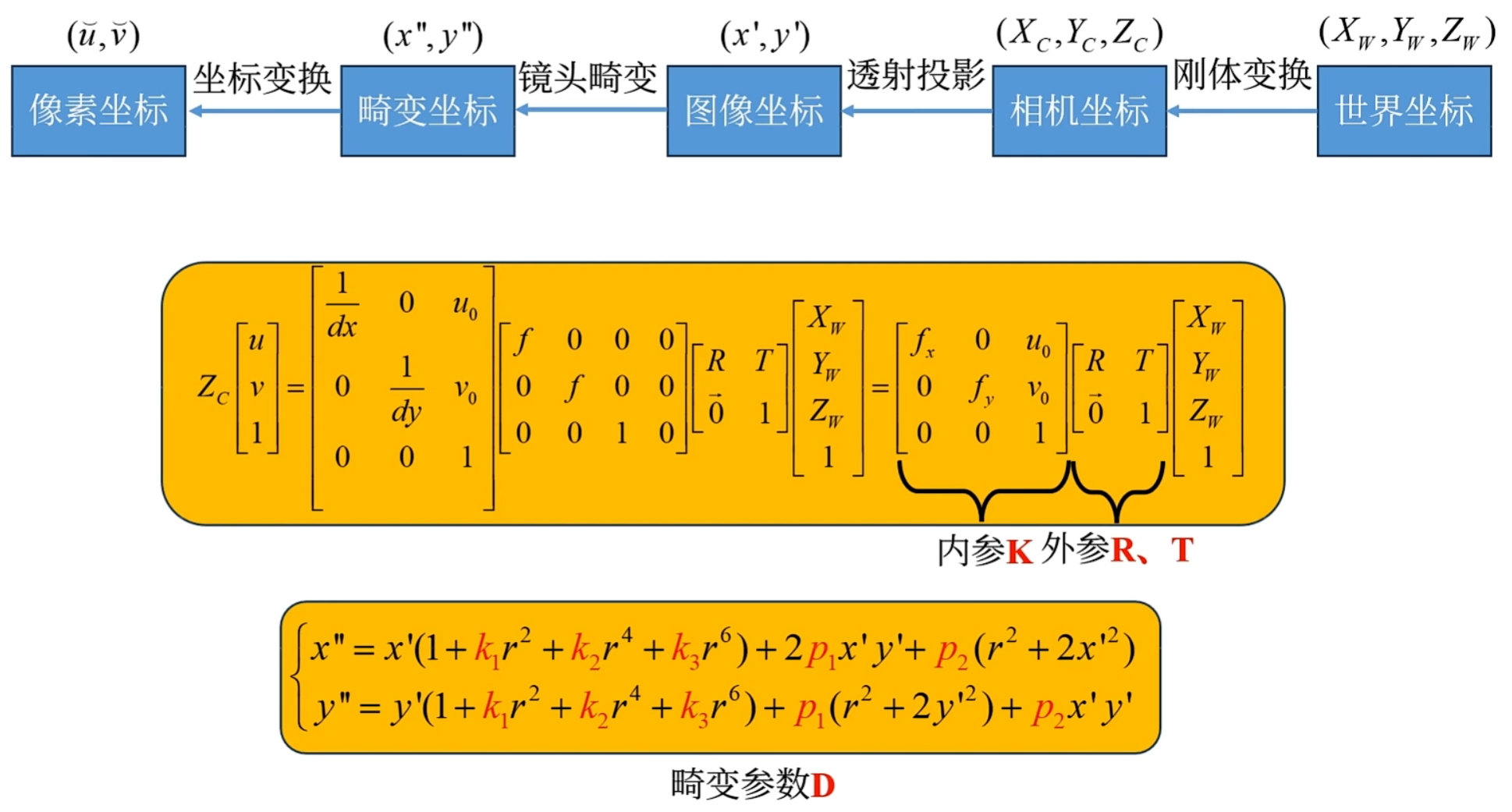
image-20250623112914367

张正友标定法

现在对于相机最常用的方法是张正友标定法，这种方法是利用棋盘格标定板每个角点像素坐标的相对关系以及在已知的真实坐标相对关系的条件下计算出来的。在opencv中已经有了相对于的库，在使用之前需要设置一下每个格子的大小以及格子的行列数（减去1）即可进行相机标定。

3

  1. 用二维靶标代替三维标靶

  2. 用棋盘格的角点作为特征点

    image-20250623114200328

  3. 张正友标定只考虑了径向畸变，没有考虑切向畸变

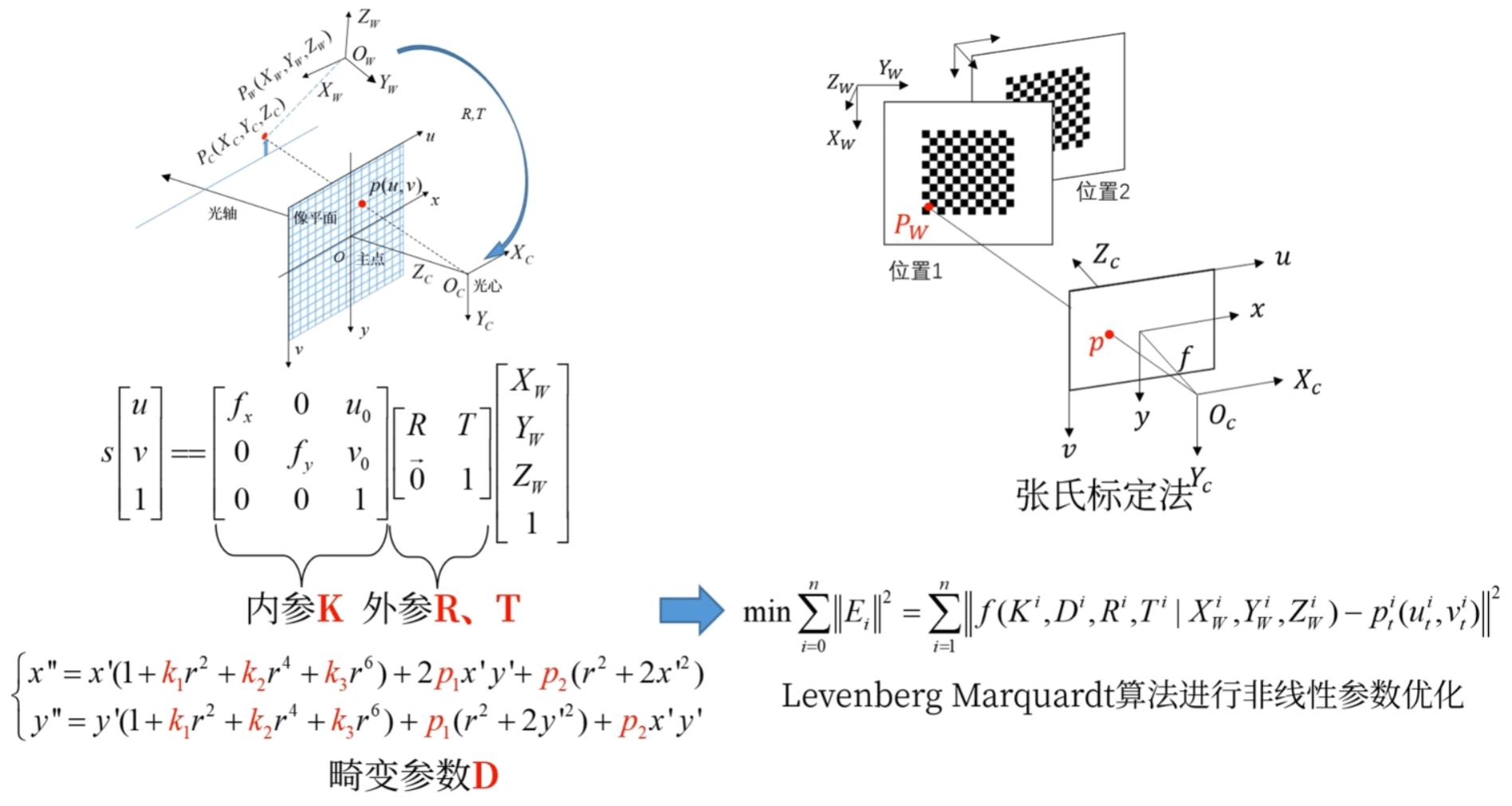
image-20250623114327451

标定步骤

image-20250623114434865

打印标定板 -> 从不同角度拍摄 -> 提取特征点 -> 估计无畸变情况下的五个内参和六个外参 -> 估计畸变参数 -> 最大似然法进行联合优化 -> 相机内参、外参、畸变参数

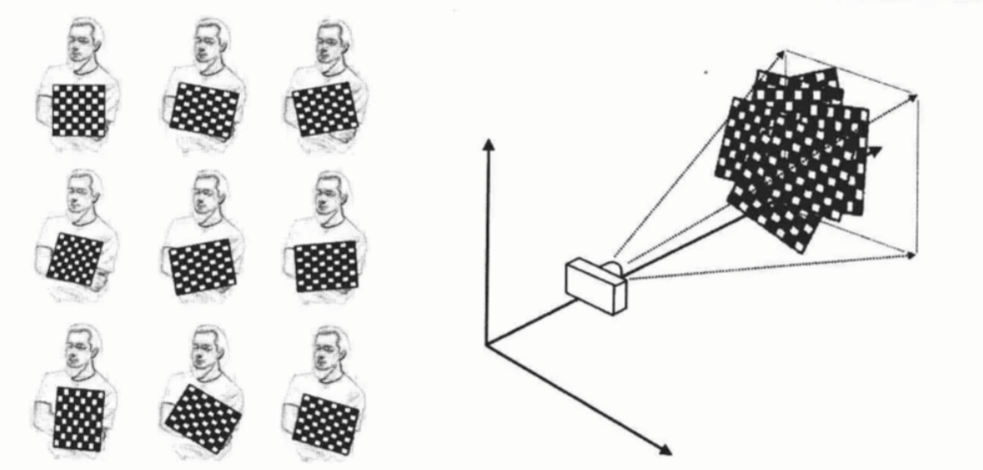
标定图像的选择

常见的标定图案有棋盘格、圆、圆环，对于普通相机一般使用棋盘格就可以了

标定板注意事项

  1. 棋盘格的大小要合适，不能太小也不能太大，保证标定板的成像面积大致占整个画面的1/4
  2. 棋盘格内角点行列个数最好不一致，比如7*8
  3. 须保证打印的棋盘格的平整性，尽可能贴平

参数个数

  1. 总参数个数: 5个相机内参(也有说4个的)，3个旋转角度、3个平移，5个畸变参数

  2. 相机内参: f,dx,dy,u0,v0(fx,fy)，旋转:(α,Ψ,@)，平移:tx,ty,tz，畸变(kl,k2,k3,pl,p2)

  3. 不同的棋盘格图像，外参是不同的，一般外参指的是第一张图像的旋转平移参数

拍摄注意事项

  1. 把图像分成四个象限，标定板平均分布在每个象限，每个象限至少拍两个不同倾斜角度的图片
  2. 标定板图片需要覆盖整个测量视场，标定图片的数量通常在15~25张之间
  3. 标定板的成像面积应大致占整幅画面的1/3~1/4
  4. 标定板成像过暗就需要用辅助光源补光，过亮就调整曝光时间，保证标定板的亮度足够且均匀
  5. 标定过程，相机的光圈、焦距不能发生改变改变需要重新标定

重投影误差

标定后每个三维点根据相机的投影矩阵计算得到的图像位置与实际图像位置之间总存在一个距离，这个距离的累加和就是重投影误差
一般情况下如果重投影误差小于0.3pixel，我们就认为标定效果良好。