手眼标定理论与实践
手眼标定
1.术语解释
$R^{base}_{end}$: 机械臂末端坐标系到基底坐标系的旋转变换矩阵,对应cv2.calibrateHandEye()参数R_gripper2base
$T^{base}_{end}$: 机械臂末端坐标系到基底坐标系的平移变换矩,对应cv2.calibrateHandEye()参数t_gripper2base
$R^{cam}_{target}$: 标定板坐标系到相机坐标系的旋转变换矩阵,对应cv2.calibrateHandEye()参数R_target2cam
$T^{cam}_{target}$: 标定板坐标系到相机坐标系的平移变换矩阵,对应cv2.calibrateHandEye()参数R_target2cam
对一般机械臂,对于每个位姿,通常会返回六个参数:$\theta_x、\theta_y、\theta_z、t_x、t_y、t_z$,这六个参数是机械臂末端在基地坐标系下的位姿的表示。
$$
R^{base}_{end}=R_zR_yR_x
$$
$$
T^{base}_{end}=(t_x,t_y,t_z)^T
$$
变换矩阵:
$$
M^A_B
\left[
\begin{matrix}
R^A_B & T^A_B \
0 & 1
\end{matrix}
\right]
$$
$$
M^A_B = {M^B_A}^{-1}
$$
转换关系
$$
R_{base}^{end}={R^{base}_{end}}^{-1}
$$
$$
M_{base}^{end}={M^{base}_{end}}^{-1}
$$
$$
T_{base}^{end} = -{R_{end}^{base}}^{-1}T_{end}^{base}
$$
==注意==:由于R是正交矩阵,正交矩阵的逆等于正交矩阵的转置,所以有时候也会写为$R_{base}^{end}={R^{base}_{end}}^T$,但是变换矩阵M不是正交,不可以用转置表示逆
代码:
1 | # 求逆 |
$$
R_x(\theta_x)=
\left[
\begin{matrix}
1 & 0 & 0 \
0 & cos\theta_x & -sin\theta_x \
0 & sin\theta_x & cos\theta_x
\end{matrix}
\right]
$$
$$
R_y=
(\theta_x)\left[
\begin{matrix}
cos\theta_y & 0 & sin\theta_y \
0 & 1 & 0 \
-sin\theta_x & 0 & cos\theta_y
\end{matrix}
\right]
$$
$$
R_z=
(\theta_x)\left[
\begin{matrix}
cos\theta_z & -sin\theta_z & 0 \
sin\theta_z & cos\theta_z & 0 \
0 & 0 & 1
\end{matrix}
\right]
$$
通过拍摄标定板,使用cv2.solvePnp()函数,可以求得
$R^{cam}_{target}$
$T^{cam}_{target}$
2.眼在手外
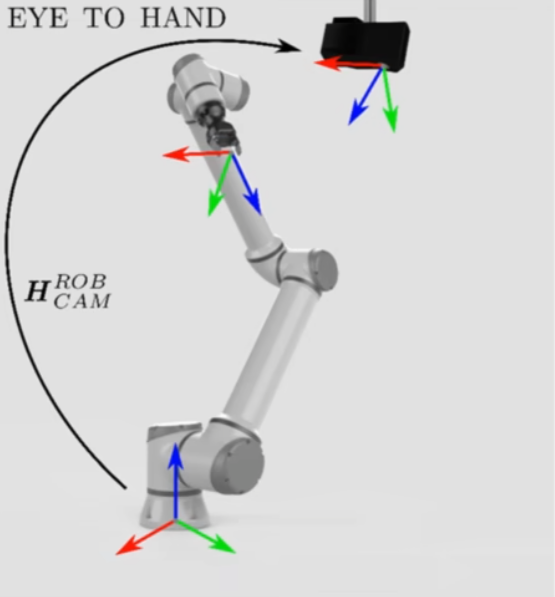
求解目标:基底坐标系到相机坐标系的变换矩阵$M^{cam}_{base}$
实现方法:
- 标定板固定在机械臂末端
- 使用相机拍摄机械臂不同姿态下的标定板图片n张(n>3)
则对于每张图片可知:
$$
M^{cam}{base}=M^{cam}{target}*M^{target}{end}*M^{end}{base}
$$
c: 相机坐标系下的坐标
b: 基底坐标系下的坐标
$$
c=M^{cam}_{base}*b
$$
$$
b ={M^{cam}_{base}}^{-1}*c
$$
其中:
$M^{cam}_{target}$: 可通过拍摄标定板图片直接求解
$M^{end}_{base}$: 可由机械臂末端位姿参数求得
$M^{target}_{end}$: ==未知量==,由于标定板固定在机械臂末端,所以对每组图片,该转换矩阵都相同
变形得:
$$
M^{target}{end}={M^{cam}{target}}^{-1}M^{cam}_{base}{M^{end}{base}}^{-1}
$$
当我们拍摄了2张图片后:
$$
{M^{cam}{target}}^{-1}1*M^{cam}{base}*{M^{end}_{base}}^{-1}_1
{M^{cam}{target}}^{-1}2*M^{cam}{base}*{M^{end}{base}}^{-1}2
$$
变形得:
$$
{M^{cam}{target}}2*{M^{cam}{target}}^{-1}1*M^{cam}{base}
M^{cam}{base}*{M^{end}{base}}^{-1}2*{M^{end}{base}}_1
$$
这是一个$AX=XA$的方程
当我们拍摄了n张图片后,我们就有了n-1个方程的方程组
通过Tais方法解方程


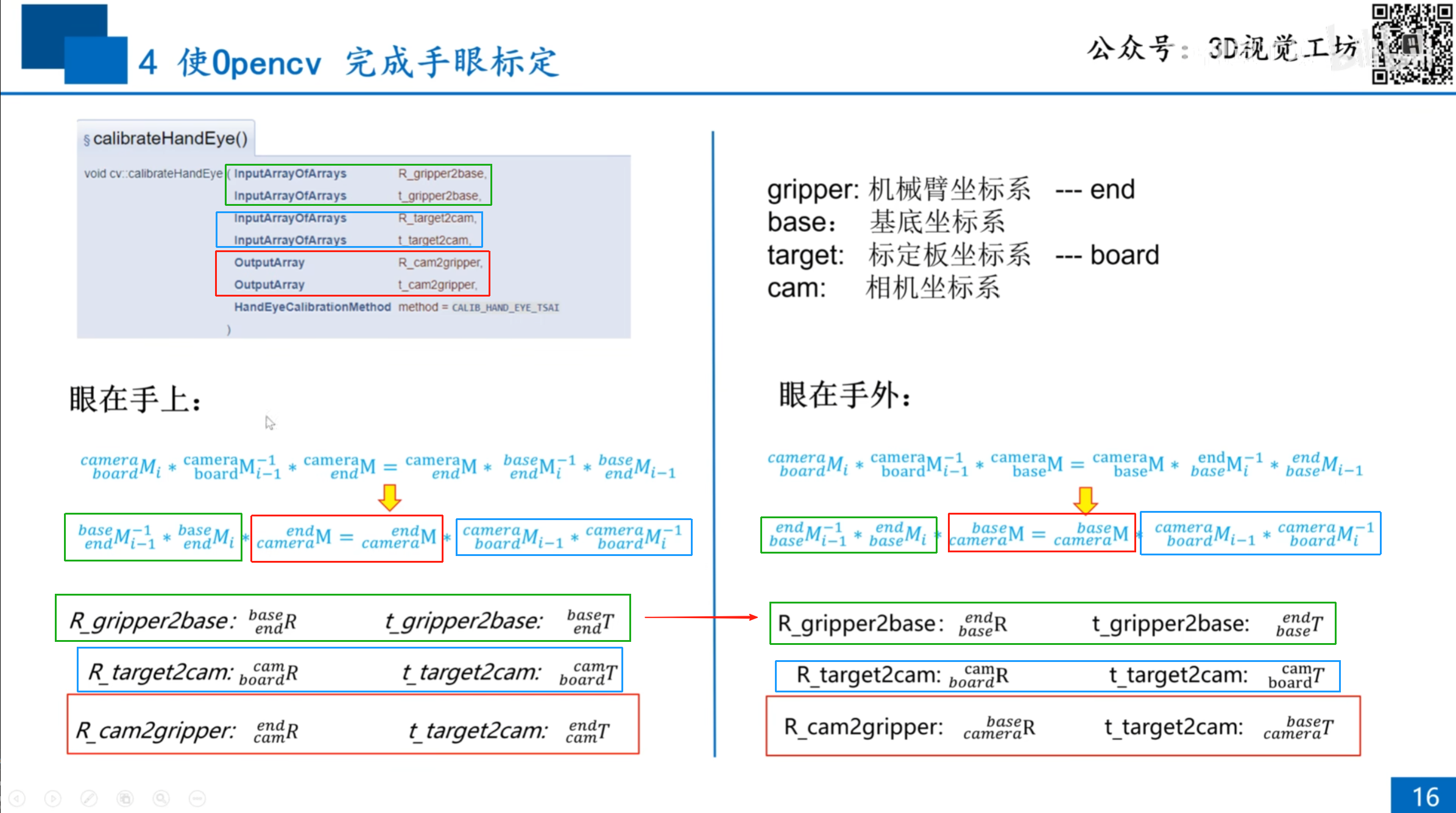
3.眼在手上
4.踩坑记录
1.标定板单位和机械臂坐标单位对齐
2.关闭相机镜像
3.不同分辨率下的标定数据不能通用